Binary Coffee

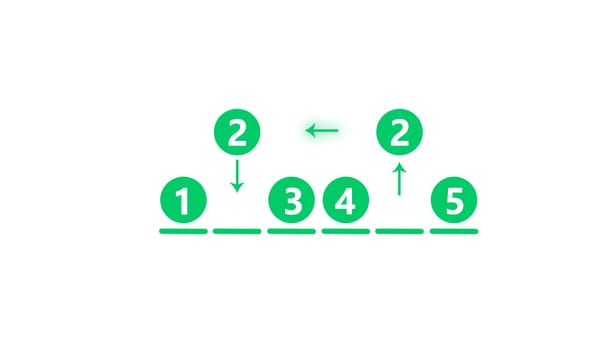
Conociendo el ordenamiento por inserción (Insertion Sort)

khozmosa year agocomment1
algorithms icpc
khozmosa year agocomment1
Relacionado
Opiniones
noavatar
// a year ago

"Frank"

Implementación en Python: https://gist.github.com/frarteaga/d1e94c782028b86f0999916f80f1d677
class Relacionado {
}
Copyright ©2021|Todos los derechos reservados
Hecho con por DC's Community
En el sitio actual se están utilizando cookies para mejorar su experiencia y mostrar anuncios que le sean relevantes.Si desea conocer un poco más sobre el tema, puede leer las políticas de privacidad y las políticas de cookies actualizadas.